Hai Wang, Jue Nan, Tao Zhang, Xingze Qiu, Wenlan Chen, and Xiaopeng Li. "Kernel function based quantum algorithms for finite temperature quantum simulation."

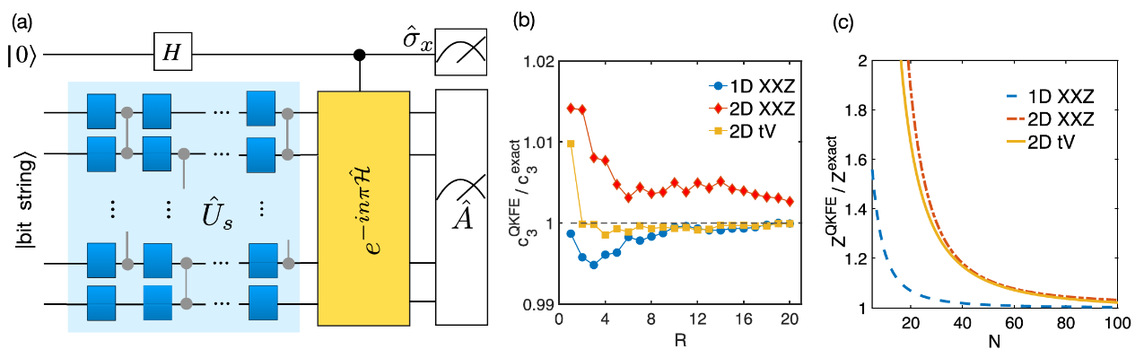
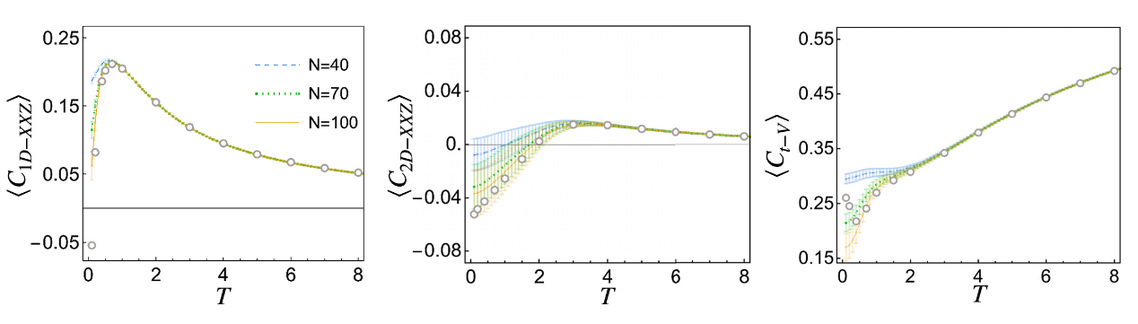
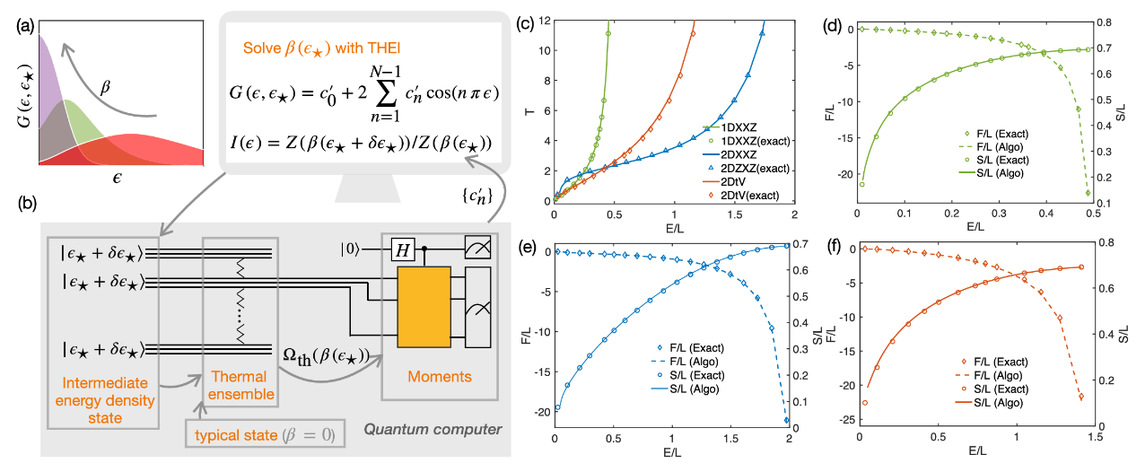
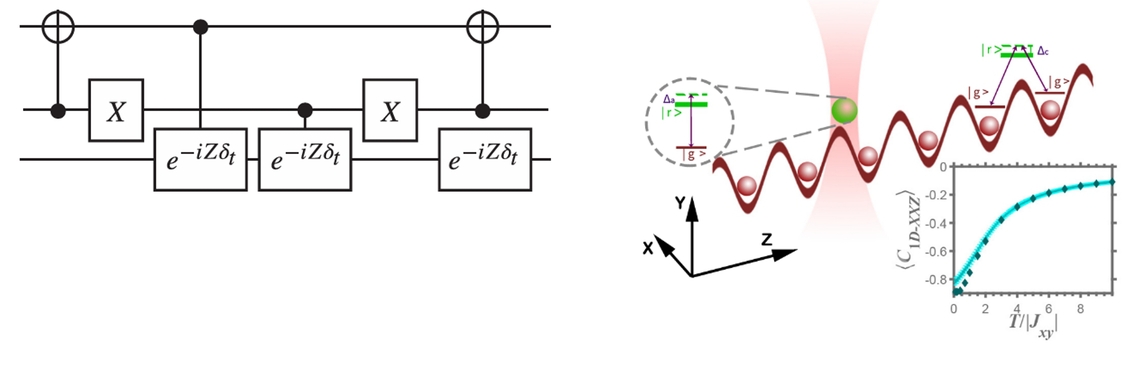
Abstract: Computing finite temperature properties of a quantum many-body system is key to describing a broad range of correlated quantum many-body physics from quantum chemistry and condensed matter to thermal quantum field theories. Quantum computing, which has seen rapid developments in recent years, has a huge potential to impact the computation of quantum thermodynamics. To fulfill these potential impacts, it is crucial to design quantum algorithms that utilize the computation power of quantum computing devices. Here, we present a quantum kernel function expansion (QKFE) algorithm for solving thermodynamic properties of quantum many-body systems. In this quantum algorithm, the many-body density of states is approximated by a kernel Fourier expansion, whose expansion moments are obtained by random state sampling and quantum interferometric measurements. Compared to its classical counterpart, namely, the kernel polynomial method (KPM), QKFE has an exponential advantage in the cost of both time and memory. In computing low temperature properties, QKFE becomes inefficient, similar to classical KPM. To resolve this difficulty, we further construct a thermal ensemble iteration (THEI) protocol which starts from the trivial limit of an infinite temperature ensemble and approaches the low temperature regime step by step. For quantum Hamiltonians, whose ground states are preparable with polynomial quantum circuits, THEI has an overall polynomial complexity. We demonstrate its efficiency with applications to one- and two-dimensional quantum spin models and a fermionic lattice. With our analysis of the realization with digital and analog quantum devices, we believe the quantum algorithm is accessible to current quantum technology.