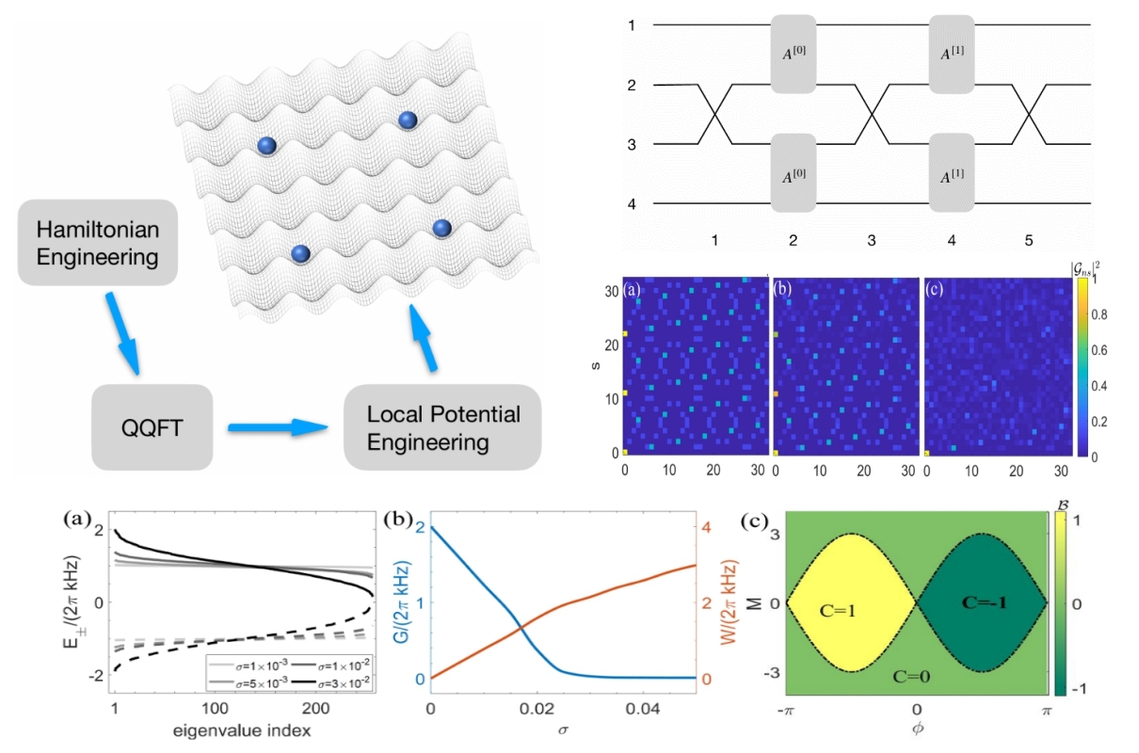
Our group has been making continuous efforts on Hamiltonian quantum simulations. There are two main themes of performing Hamiltonian quantum simulations. One is to use controllable quantum systems to simulate novel quantum many-body physics such as exotic quantum states, unconventional quantum dynamics, and intriguing quantum entanglement. In fact, various topological states including topological insulators, and semimetals have been engineered using quantum simulation platforms. The temporal crystalline order has been observed with trapped ions and superconducting qubits. These studies have substantially enriched our view of low-temperature quantum phenomena. The other theme is to use quantum simulation to solve computationally difficult problems, ranging from strongly correlated Fermi-Hubbard models and high-Tc superconductivity to lattice gauge theories and high-energy physics. Our research interest was focusing on the former several years back, and the present focus is more towards the latter.

We also develop a generic recipe for performing quantum simulation of all translationally invariant quantum tunneling models, regardless the existence of long-range couplings. This is based on our constructed quadratic quantum Fourier transform, a variant of the well-known quantum Fourier transform. The algorithmic approach to perform Hamiltonian quantum simulations is highly flexible, enabling quantum simulations of Poincaré crystals and completely-flat topological bands, which are almost impossible to implement with other approaches.