Atomic Quantum Computing

One current focus of our group is to build atomic quantum computers using atomic tweezer arrays. We have cooled Rb, and Li atoms down to 0.1mK or even lower temperatures. These cold atoms are confined in optical tweezers, focused to their diffraction limit, with the beam widths around 1μ m. Each atom can be controlled and probed individually. We take the magnetically insensitive hyperfine states as atomic qubits, and construct large-scale quantum computers. We are developing technologies for controlling multiple atomic species in a single high vacuum chamber, making a heteroatom quantum computer. This gives extra flexibility for mid-circuit quantum measurement and fault-tolerant quantum computing.

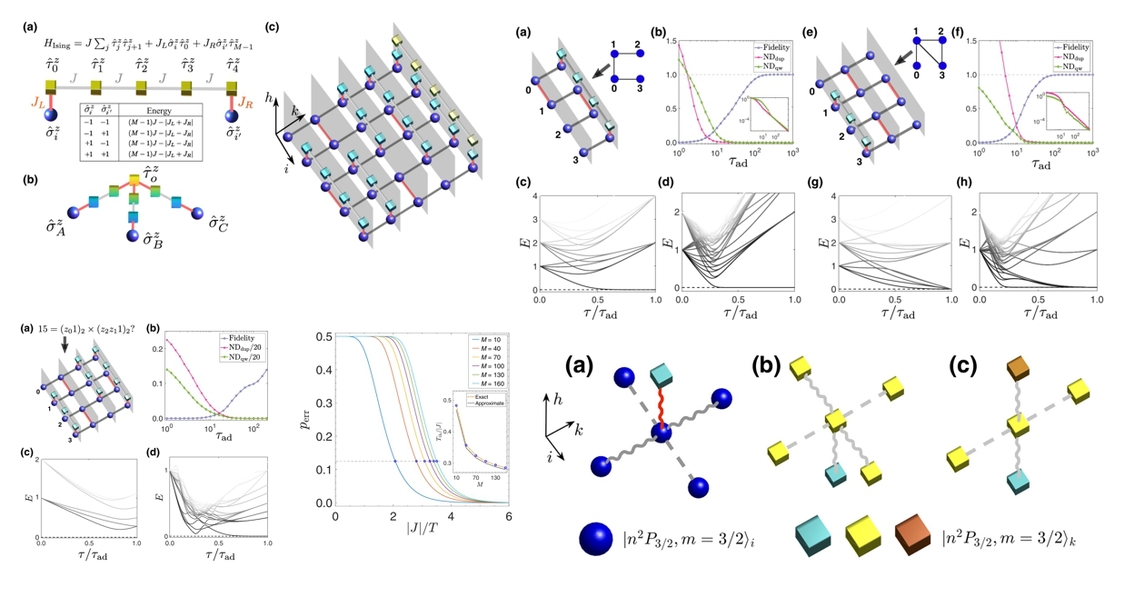
We have developed a quantum wiring scheme, for implementing quantum optimization with atom arrays. With this scheme, any discrete optimization problems can be encoded by local Ising models on a cubic lattice, which has a natural realization with Rydberg atoms. This has been adopted by experimental groups for solving difficult graph partition, factorization, and MaxCut problems, which circumvent fundamental connectivity-limitations in previous encoding schemes. 

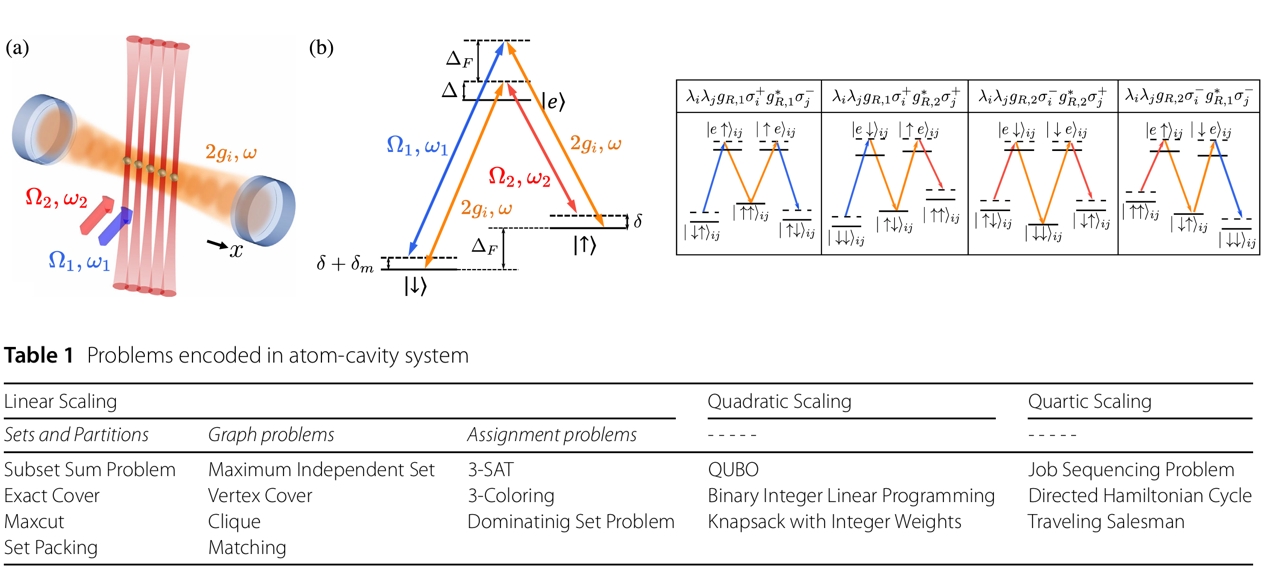
We have systematically investigated the computation power of the atom-cavity system. This system naturally encodes the computation problem of number partition, which implies obtaining the ground state of the atom-cavity system is NP-hard. We show the atom-cavity system is more powerful in solving NP-problems than Rydberg atoms—a variety of NP-hard problems that cannot be encoded efficiently by Rydberg atoms can be encoded by the atom cavity, including 3-SAT, MaxCut, vertex-cover, 3-coloring.